Ｅ資格挑戦！！

このブログはＥ資格取得に向けた学習内容をまとめたものです(^o^）

トップ > Ｅ資格 > 応用数学【ラビット・チャレンジ（E資格）】

応用数学【ラビット・チャレンジ（E資格）】

Ｅ資格

第１章：線形代数

要　点

　本章は機械学習に必要な応用数学のうち線形代数学に係る内容が主題である。

　講義ではスカラー、ベクトルその計算方法等について概説したのち、特に下記の４項目（①〜④）について、説明と実習（例題演習）が行われた。

 

スカラー

　・ いわゆる普通の数

　・ ＋、ー、×、÷の演算が可能

　・ ベクトルに対する係数になれる。

ベクトル

　・ 「大きさ」と「向き」をもつ

　・ 矢印で図示される。

　・ スカラーのセットで表示される。

 行列

　・ スカラーを表にしたもの

　・ ベクトルを並べたもの（ベクトルのベクトル）

　 　▶　ベクトルの変換に使う。

 

行列の積の計算

　行列の「行」×「列」から新たな行列成分を算出　　　f:id:satoshi19841011:20210218135918p:plain

　計算例

　f:id:satoshi19841011:20210218140019p:plain

単位行列

　掛けても掛けられても相手が変化しない「１」のような行列を単位行列という。単位行列とその計算例は下記の通り。

　　f:id:satoshi19841011:20210218141020p:plain

逆行列

　逆数のように元の行列とかけることで「１」（単位行列）になるような行列。計算例は下記の通り。　

　　f:id:satoshi19841011:20210218141059p:plain

①　固有値・固有ベクトルの求め方

　ある正方行列Aに対して，以下の式が成り立つベクトルxと，係数λがあるとき、ベクトルxを固有ベクトル、λを固有値という。　　　　　　　　　　　　　　

f:id:satoshi19841011:20210202090013p:plain

　　　　

②　固有値分解の理解

　　行列Aが固有値、

            f:id:satoshi19841011:20210202090858p:plain

　　対応する固有ベクトル、

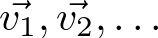
            \begin{align*} \vec{v_{1}}, \vec{v_{2}}, \dots\\ \end{align*}　　　

  　　を持つとき、固有値を対角線上に並べた行列（それ以外の成分は0）

           \begin{align*} A=\left(\begin{array}{ccc} \lambda_{1} & {} & {}\\ {} & \lambda{2} & {} \\ {}&{}&{\ddots} \end{array} \right) \end{align*}

　　と，それに対応する固有ベクトルを並べた行列

           \begin{align*} V=\left(\begin{array} {CCC} \vec{v_{1}}, & \vec{v_{2}} & \dots\\ \end{array} \right) \end{align*}

　　をおくとき、次が成り立つ。

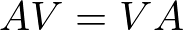
           \begin{align*} AV=VA \end{align*}

　　これを変形すると、次の式が得られる。

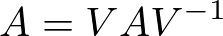
           \begin{align*} A=VAV^{-1} \end{align*}

　　このように正方形の行列を上述の様な３つの行列の積に変換することを固有値分解

という。この変換によって行列の累乗の計算が容易になる等の利点がある。

 


③　特異値・特異ベクトルの概要　／　④特異値分解の理解

　正方行列でない行列Mに対し、次のような固有ベクトルがあれば固有値分解できる。

 　\begin{align*} M \vec{v}=\rho \vec{u}\\ M^{T} \vec{u} = \rho\vec{v} \end{array} \right) \end{align*}

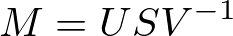
    \begin{align*} M=USV^{-1} \end{align*}

　このとき、次が成り立つ。

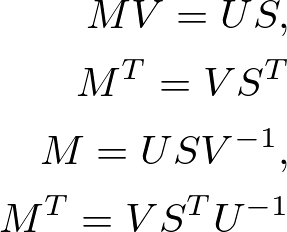
\begin{align*} MV=US,\\ M^{T}= VS^{T}\\ M=USV^{-1},\\ M^{T}=VS^{T}U^{-1} \end{align*}

さらに、

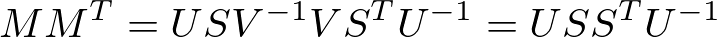
\begin{align*} MM^{T}=USV^{-1}VS^{T}U^{-1}=USS^{T}U^{-1} \end{align*}

左辺を固有値分解すれば，その左特異ベクトルと特異値の2乗が求められる。

計算例を下記に示す。

f:id:satoshi19841011:20210202102908j:plain

 

　固有値・固有ベクトル等の行列の計算方法自体は、やり方を覚えれば手計算でも難しくない印象である。一方、固有値分解の適用により、行列の累乗計算が容易になる等、計算機上の実装を見据えた行列の性質を理解しておくことの重要性を感じた。

関連記事レポート

　本章の内容は理系大学の１年生で履修する線形代数学の講義内容と多くの共通部分がある。そのため、インターネット上に様々な大学の講義資料があり、理論的に深堀したい場合は有用である（「線形代数 pdf 講義」などで検索すると多くの大学のHPでpdf形式の講義資料が公開されている。）。私自身も理系大学出身ではあるが、大分忘れている部分があり、復習を兼ねて閲覧した。

　また、計算結果の検算には下記にリンクを貼った"WolframAlpha"も活用した。今後、Python上で様々な計算を実装すると思うが、確認用として活用していきたい。

www.wolframalpha.com

www.wolframalpha.com

第２章：確率・統計

要　点

　本章は機械学習に必要な応用数学のうち統計学に係る内容が主題である。

　機械学習では大量のデータからの特徴の抽出・分析が必要であり、それらを理解する上で統計学の知識が不可欠である。講義では、「集合」、「確率」、「統計」について解説があった。

 「集合」

　講義では最初に基本的な「集合」の概念とその表現方法（和集合、補集合、それらを使用した集合の表現など）の説明と例題演習がなされた。内容的には高校数学の内容がメインである。集合に用いる記法やベン図を用いた表現を良く思い出す必要があると感じた。 

 「確率」

　講義では確率の定義に始まり、その計算方法について概要説明と実習（例題）が行われた。特に「条件付き確率」は前述に「集合」におけるベン図を併用することで視覚的に分かりやすくなることが示されていた。

f:id:satoshi19841011:20210202112618j:plain

　また、例題としてベイズ則を利用して、複数の条件下で特定の事象が発生する確率を計算した。

　例題：ある街の子どもたちは毎日1/4の確率で飴玉をもらうことができ，飴玉をもらうと1/2の確率で笑顔になるという。その街の，笑顔な子どもが飴玉をもらっている確率を求めよ。(ただし，この街の子どもたちが笑顔でいる確率は1/3である。)

f:id:satoshi19841011:20210202112719j:plain

 

 「統計」　

　講義では統計のうち記述統計を主題として、関連する用語の定義、説明がなされた。具体的には、確率変数・確率分布、期待値、分散、標準偏差などである。これらは機械学習で大量のデータを分析する上で基礎となる考え方・定義である。　

f:id:satoshi19841011:20210202112831j:plain

f:id:satoshi19841011:20210202112852j:plain

　また、上記の確率分布には対象となるデータの種類、散らばり方などによりベルヌーイ分布（コインの裏表確率等）、マルチヌーイ分布（サイコロの目の確率等）、特に実用的な分布として二項分布、ガウス分布などがある。さらに、一部のデータ（標本）をもとに全体（母集団）を推定する上で必要となる指標（標本分散、不偏分散）の計算とその意味について理解した。

f:id:satoshi19841011:20210202112505j:plain



関連記事レポート

　本章の内容は理系大学の１〜２年生で履修する統計学の講義内容と多くの共通部分がある。そのため、インターネット上に様々な大学の講義資料があり、理論的に深堀したい場合は有用である（「統計学 pdf 講義」などで検索すると多くの大学のHPでpdf形式の講義資料が公開されている。）。統計学は理系大学の講義のみならず、データ分析の観点からビジネスの場でも注目されている。　　

 

www.amazon.co.jp

第３章：情報理論

要　点

　情報理論では情報の表現方法（定義の仕方）を検討対象としている。

　講義では、単純な数量の比較ではなく数量の増加率を情報量の増加として説明し、この際の情報量について対数を用いて自己情報量という式で定義している。さらに自己情報量の期待値（講義では「情報の珍しさ」と表現）をシャノンエントロピーという式で示している。シャノンエントロピーでは、自己情報量とそれが起こる確率を掛けたものの総和で示されている。

　裏表のあるコイントスで例えると、情報量が最大になる値は0.5（裏表の確率が各0.5）である場合である。仮に情報量が0であれば、コインは常に表（又は裏）しか出ないことになり、コイントスにより得られる情報は0（情報量が0）ということになる。

　その他、同じ事象・確率変数であるのに関わらず確率分布が異なる場合の評価方法であるカルバック・ライブラ− ダイバージェンスや、交差エントロピーの考え方、計算式についても説明がなされた。

f:id:satoshi19841011:20210202112312j:plain

関連記事レポート

　情報量の考え方の理解を深めるため、関連するHP等を検索した。

　下記HPは講義にもあったコイントスの例のほか、「くじ引き」を例にした説明もあり、本講義の理解を深める上で有用であったと思う。また、今後Pythonを利用して機械学習等を実装することを考慮し、Pythonでの計算の実装を含め参考にしたい。

pystyle.info